/ Back / Home /
The Algorithm
Radix (or base) is a latin word that means root. It is the number of unique digits used to represent a number. For example, for decimal numbers radix = 10, for binary radix = 2, for hexa radix = 16 and so on. Radix-sort is a distribution (non-comparison) sorting algorithm that sorts a collection of elements.
Radix sort is suitable to sort large set of integers, but since it treats integers as strings of digits it is in fact a string sorting algorithm. There are 2 flavors:
- LSD Radix Sort (Least Significant Digit Radix Sort): numerical sort
- MSD Radix Sort (Most Significant Digit Radix Sort): lexicographic sort
Note that strings and numbers have different representations:
- Numbers are always represented from right to left with the unit place: tens, hundreds… etc (numerical sort example: 01, 02, 10)
- The alphabetical words (strings), the place is always relative to the longest word from left to right (alphabetical sort example: 1-, 10, 2-)
Description of LSD Radix Sort
LSD Radix-sort sorts a collection of integers by distributing them according to the value of the digits into buckets and then place them back in sorted order. Thus, each digit is considered starting from the least significant to the most significant. For each digit, elements are distributed into buckets, so each element is distributed into the bucket that represents the value of the current digit. After distribution, the elements are placed back in the collection, elements being sorted relative to the current digit, and in case the current digits are equal, it is preserved the order from the previous digit (i.e. stable sort).
See below the graphical representation of LSD Radix Sort:

Implementation
LSD Radix Sort for integers
void sort(vector<int>& a, int k) {
if (a.size() <= 1) return;
for (int d = 0; d <= k; d++) {
radixSortCount(a, d);
}
}
void radixSortCount(vector<int>& a, int d) {
vector<int> b(a);
int n = (int)b.size();
int radix = 10;
int D = (int)pow(radix, d);
// distribute to buckets
vector<int> count(radix, 0);
for (int i = 0; i < n; i++) {
int digit = (b[i] / D) % radix;
count[digit]++;
}
// counters to indexes
for (int i = 1; i < radix; i++)
count[i] += count[i - 1];
// place items in sorted order
for (int i = n - 1; i >= 0; i--) {
int digit = (b[i] / D) % radix;
a[count[digit] - 1] = b[i];
count[digit]--;
}
}
MSD Radix Sort for strings
void sort(vector<string>& a) {
if (a.size() <= 1) return;
int maxLen = getMaxLen(a);
for (int d = maxLen - 1; d >= 0; --d) {
radixSortCount(a, d);
}
}
void radixSortCount(vector<string>& a, int d) {
vector<string> b(a);
int n = (int)b.size();
int radix = 256;
vector<int> count(radix, 0);
// distribute to char buckets
for (int i = 0; i < n; i++) {
int index = (d < b[i].length() ? b[i][d] : 0);
count[index]++;
}
// counters to indexes
for (int i = 1; i < radix; i++)
count[i] += count[i - 1];
// place items in sorted order
for (int i = n - 1; i >= 0; i--) {
int index = (d < b[i].length() ? b[i][d] : 0);
a[count[index] - 1] = b[i];
count[index]--;
}
}
int getMaxLen(vector<string>& a) {
int m = INT_MIN;
for (string s: a) m = max(m, (int)s.length());
return m;
}
Complexity Analysis
Time Complexity
Because the stable sort is called \(k\) times, the time complexity of Radix sort is \(\Theta(k*T_{stable-sort})\). If Counting-sort is used as a stable sort (having the complexity of \(\Theta(n + radix))\), then the time complexity of Radix sort is \(\Theta(k * (n + radix))\), so \(T(n) = O(k * n)\), where \(k\) is the number of digits and \(n\) is the size of the collection.
Space Complexity (auxiliary)
\(S(n) = O(n + radix)\) since we need an auxiliary array of size \(n\) and an array of buckets of size \(radix\).
Applications of Radix Sort
-
Sorting by multiple keys.
If we have a set of records and if we want to sort them by a key composed of several fields, for example, suppose we have a key made up of {year, month, day} and we want to sort by date. A variant is to use Radix Sort to sort a key of the form YYYY.MM.DD. Another option is to use qsort and when comparing 2 records per year and there is a tie, then compare on month, if tie on month then compare on day.
-
Card sorting machines.
It was used to sort 12-row/80-column IBM punched cards. Thus, the operator could collect the cards that had a hole on row 1, then on row 2…etc. Radix sort sorts the cards by rows and then by columns.
-
When \(log_{2}n >> w\), where w is the word size of the machine
The basic question is: why not Radix Sort instead of Quicksort?
Quicksort has a complexity of \(nlog_{2}n\) and Radix sort has a complexity of \(O(k*n)\). Radix sort becomes an alternative when \(k*n < nlog_{2}n\), that is \(k < log_{2}n\), where k is actually the word size of the machine where the algorithm runs. So, if we have a machine with a word size of \(\Theta(log_{2}n)\) then Radix Sort has a complexity \(T(n) = O(nlog_{2}n)\), basically qsort . If we take into account the fact that Radix sort has a much higher space complexity than qsort, and qsort uses hardware caches more effectively, then in real life applications qsort outperforms Radix sort. However, if \(n >> 2^w\) (where w is the word size of the machine) then Radix sort becomes a viable solution.
Note: To understand better the paragraph above I suggest to implement Radix sort for base = 2 and word size = 32 and do the math. -
It is a good option for sorting numbers (or strings) in lexicographical order.
See MSD Radix sort above.
-
It can be used for suffix array construction. For example, suffix arrays are used to find the longest repeating substring (LRS).
To find the longest repeating substring (LRS) in a given string, you can use suffix trie or Kasai’s algorithm. If the suffix trie is used, then LRS is the deepest node in the trie that has more than one child (see the picture below). In the case of Kasai’s algorithm, the suffix array is generated using Radix sort and the LRS is the longest common prefix among all common prefixes between all consecutive suffix pairs (see the picture below).
LRS for ‘xbabab’ using suffix trie and Kasai algorithm: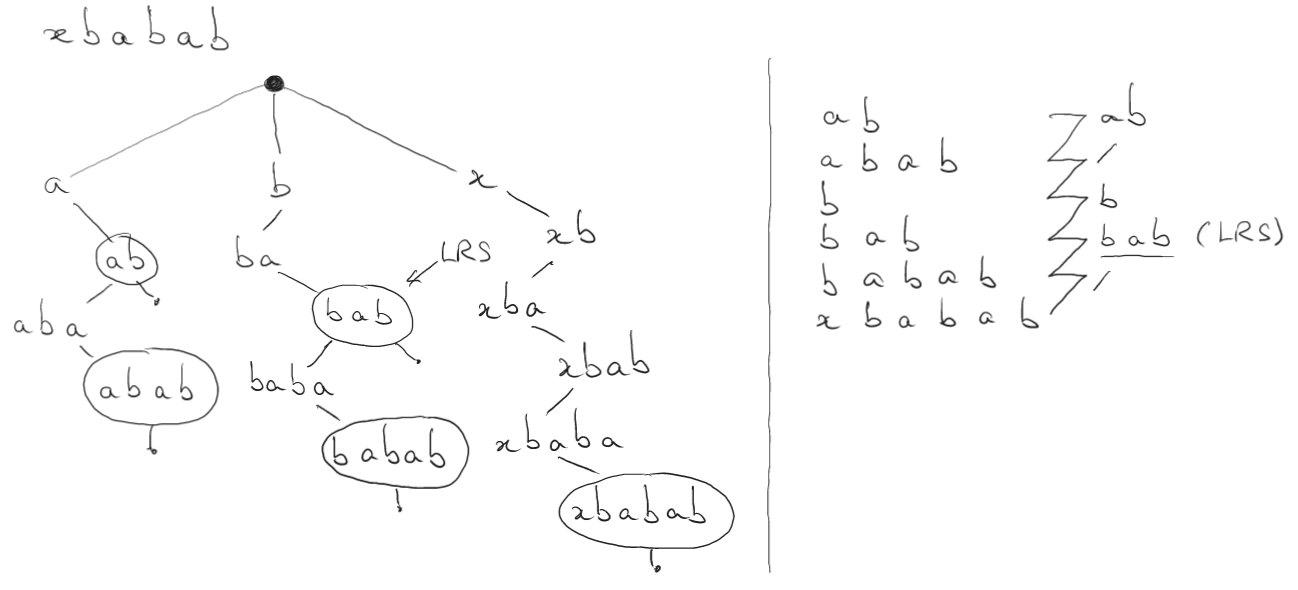
Time complexity is \(T(m) = O(m^2)\) regardless of which method is used, but suffix trie needs more memory. however we can use compressed suffix trie. -
It is a good option if the algorithm runs on parallel machines (Parallel LSD Radix Sort).
A sketch of this algorithm would sound something like this:
Step 1. Distribute data across processors (or machines)
Step 2. Each processor/machine locally sort data according to i-th digit
Step 3. Redistribute data so that the entire (concatenated) set is sorted globally according to i-th digit
Step 4. Repeat from step 2 for t+i-th digit
Note: Redistribution can be done in multiple ways (depending on how the communication between processors/machines is made). One way to redistribute could be like this: each processor knows how many numbers has for each value of the current digit and it shares this info with the other processors, so this way each processor knows from which and where to send data to achieve a globally ordered sequence according to that current digit.
Parallel LSD Radix Sort using 3 processors: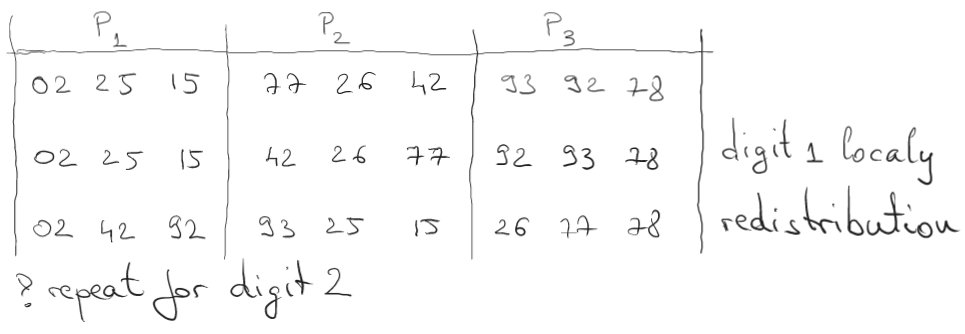
Stability
LSD Radix sort must be stable to work properly, but MSD Radix sort can also be unstable. Both the above implementations are stable, because they both uses counting sort as sorting subroutine (which is stable).
/ Back / Home /