/ Back / Home /
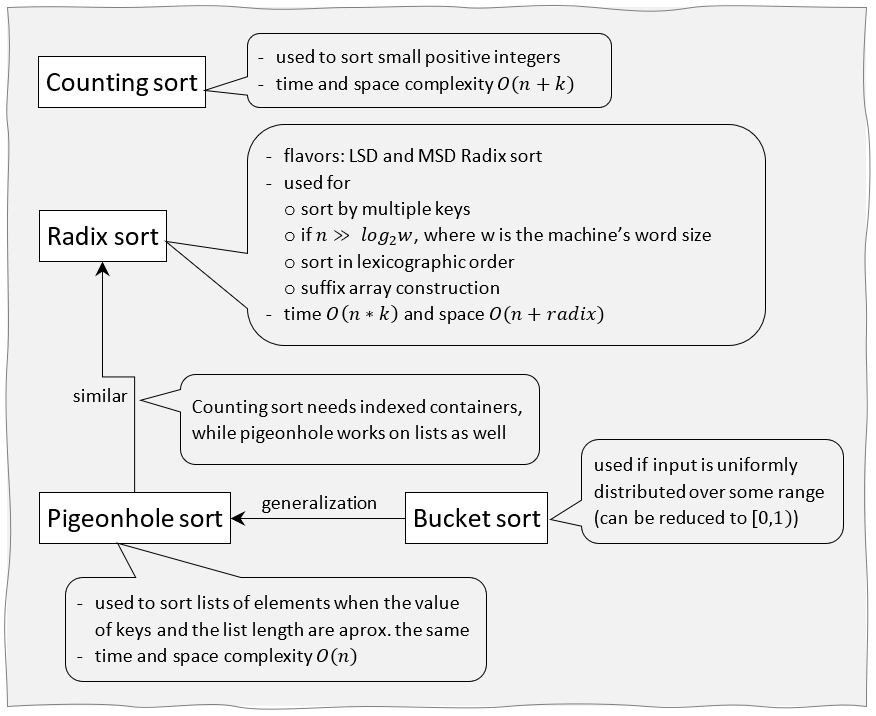
Distribution Sorting is a class of algorithms that sorts a set of items in linear time, but the input data must satisfy some special constraints. Basically, the items can be sorted faster than comparison-sort whenever the input data can be redistributed to intermediate bins and then collected in order and placed on output. Follow the links below for the algorithms that falls in this class: Counting sort, Radix sort, Bucket sort and Pigeonhole Sort. A short note: each of these algorithms imposes a different set of constraints to input data, thus each of them addresses a very narrow class of problems.
It is worth mentioning that on machines with multiple processing units these methods become really interesting because the intermediary bins can be placed on different units and sorted in parallel, thus the time complexity is improved considerably.
Complexity Table:
| Algorithm | Time complexity | Space aux. | Stable |
|---|---|---|---|
| Counting sort | \(O(n+k)\), k - upper limit | \(O(n+k)\) | yes |
| Radix sort | \(O(k*n)\), where k is the #digits | \(O(n+radix)\) | yes |
| Bucket sort | \(O(nlog_{2}n)\) - worst, \(O(n)\) - avg | \(O(n)\) | yes |
| Pigeonhole sort | \(O(n+k)\), k - range of keys | \(O(n+k)\) | yes |
Table legend: the first column contain the time complexity in the worst, average and best cases, the second column the auxiliary space complexity, and the third column the stability of the algorithm.
Note: Stability means that 2 equal keys keep relative order after sorting (eg 5 4 4’ 2 => 2 4 4’ 5: 4’ comes after 4 before and after sorting).
Quick view:
/ Back / Home /