/ Back / Home /
The Algorithm
The Merge-sort algorithm is a sorting algorithm that uses the divide and conquer method. It has three main steps as follows:
- Step 1: Divide: the given sequence is divided in half;
- Step 2: Conquer: each half is sorted recursively;
- Step 3: Combine: the two sorted halves are merged, thus the initial sequence is sorted.
Note: Several versions of Merge-sort with detailed analysis can be found in [Knuth “The Art of Computer Programming” – third volume].
Description
The algorithm can be implemented recursively or iteratively using a stack. Both implementations can be found below. The iterative variant has several advantages, for example, in practice it is somewhat faster, and the stack-overflow can be avoided/controlled more easily by throwing an exception when a certain stack occupancy threshold is reached. However, for the sake of simplicity, I will consider the recursive version, because is more intuitive and simpler to implement.
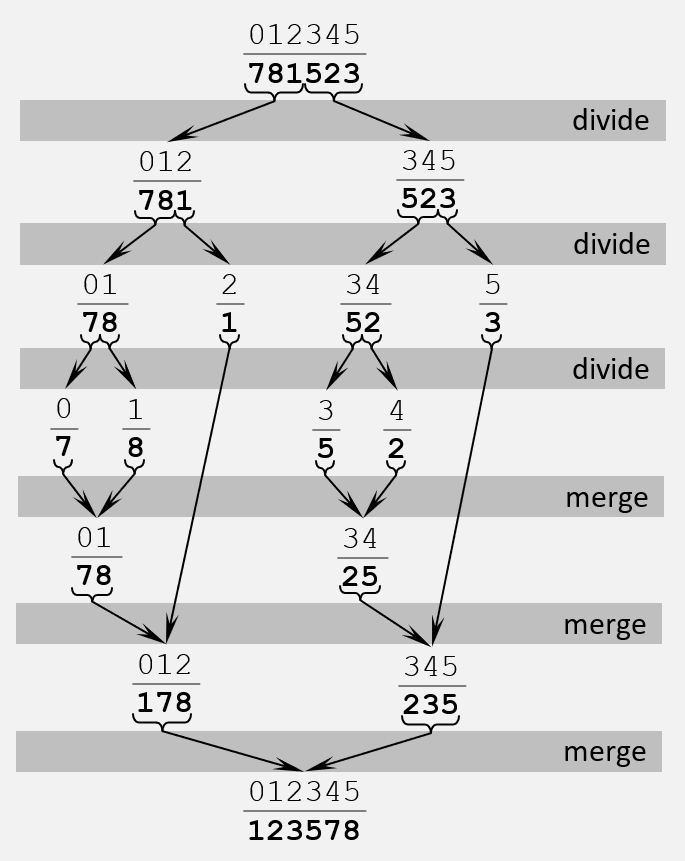
So, the given sequence is halved recursively until only one element remains (the base case), then upon return the sorted halves are merged into the single sorted sequence. Looking at the algorithm below, the divide and conquer steps are implemented by the merge and sort procedures. The initial call parameters of sort procedure are \(0\) as start and \(length-1\) as end, thus the algorithm sorts the entire sequence.
See below an execution example:
Implementation
Recursive version
void sort(vector<int>& a, int s, int e) {
if (e - s <= 1) return;
int m = (s + e) / 2;
sort(a, s, m);
sort(a, m + 1, e);
merge(a, s, m, e);
}
void merge(vector<int>& a, int s, int m, int e) {
vector<int> L(a.begin() + s, a.begin() + m);
vector<int> R(a.begin() + m, a.begin() + e);
// merge L and R so that a from s to e is sorted
int k = s, i = 0, j = 0;
while (i < (int)L.size() && j < (int)R.size())
if (L[i] < R[j]) a[k++] = L[i++];
else a[k++] = R[j++];
// add tail of L or R (if any)
while (i < (int)L.size()) a[k++] = L[i++];
while (j < (int)R.size()) a[k++] = R[j++];
}
Iterative version
void sort(vector<int>& a) {
if (a.size() <= 1) return;
stack<pair<int, int>> st; st.push(make_pair(0, a.size()));
pair<int, int> p = make_pair(-1, -1);
// postorder traversal of indexes
while (!st.empty()) {
pair<int, int> n = st.top();
int s = n.first, e = n.second;
if (e - s <= 1) st.pop();
else {
int m = (s + e) / 2;
// if the right side was previous visited, then both halves are sorted, so merge them
if (p.first == m && p.second == e) {
merge(a, s, m, e);
st.pop();
}
else {
st.push(make_pair(m, e));
st.push(make_pair(s, m));
}
}
p = n;
}
}
Correctness
The main thing that needs to be proven for the correctness of this algorithm is the merge step. Before merging, the 2 halves (which are already sorted) are copied into 2 arrays L and R, respectively. Each of the 2 arrays has an index that is initialized to \(0\). Then, in the first loop, the 2 arrays are compared element by element using these indexes and the smallest element are stored in the initial array, and the index of the smallest element is incremented. When at least one of the arrays (L or R) is exhausted (i.e. all its elements are stored in the main array) the first loop ends. In the next 2 loops, leftovers from the 2 arrays are stored. Considering that at least one of them ended in the first loop determining its termination, at most one of the following 2 loops is executed. Thus, after the merge of the 2 arrays, the statement remains invariant, that is, the array resulting from the merge remains sorted and serves as input for the next recursive step.
Complexity Analysis
Time Complexity
There is no difference between best-case, worst-case, and average-case, because there is no random selection or sub-arrays of variable length. The next approximation was made, for technical convenience: \(T(n) = T\left ( \left [ \frac{n}{2} \right ] \right ) + T\left ( \left \lfloor \frac{n}{2} \right \rfloor \right ) + \Theta(n) \cong 2 \cdot T\left ( \frac{n}{2} \right ) + \Theta(n)\).
For this algorithm, the time complexity can be calculated using both the Master Theorem and the Guess-and-Confirm method, so for fun below are both.
Guess & Confirm
Guess the solution:
The recursion spans as follows:
\(T(n) = 2 \cdot T\left ( \frac{n}{2} \right ) + cn\).
\(T(\frac{n}{2}) = 2 \cdot T\left ( \frac{n}{4} \right ) + c\frac{n}{2}\).
\(T(\frac{n}{4}) = 2 \cdot T\left ( \frac{n}{8} \right ) + c\frac{n}{4}\) … and so on …
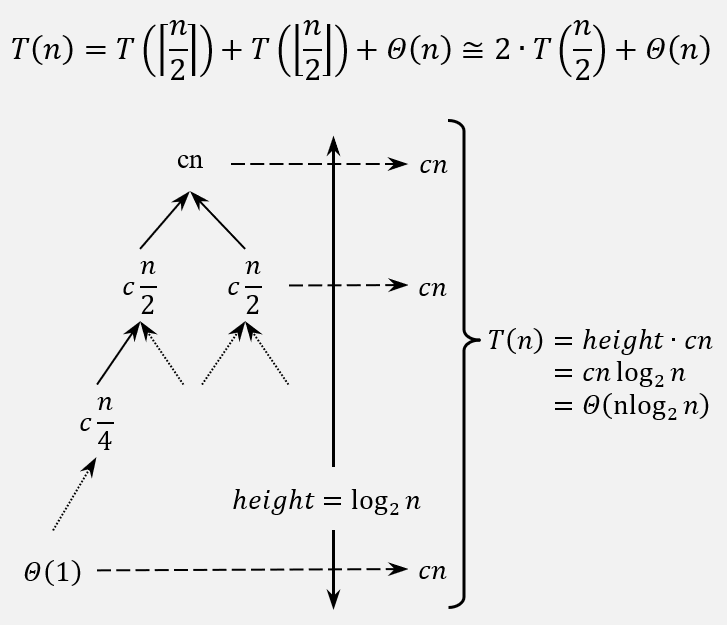
So, based on the recursion tree, the guessed solution is: \(T(n) = \Theta(nlog_{2}n)\).
Confirm by induction:
Confirm that \(T(n) \leq cnlog_{2}n\) for some appropriate constant \(c \geq 0\) and all \(n \geq n_0 > 0\).
For technical convenience let \(T(n) = 2 \cdot T\left ( \frac{n}{2} \right ) + n = \Theta(nlog_{2}n)\)
Induction’s base case
\(T(1) = 1 \Rightarrow \leq c \cdot log_{2}1 , 1 \leq 0\) – not possible
Observe that the recurrence hits either \(T(2)\) or \(T(3)\), so let these two to be induction’s base cases: \(T(2)= 4 \leq 2c \cdot log_{2}2\) – holds for \(c \geq 2\) \(T(3)= 5 \leq 3c \cdot log_{2}3\) – holds for \(c \geq 2\)
Induction’s hypothesis: assume that the inequality holds for all positive numbers less than \(n\).
Thus, it holds for all recurrence steps until and including \(T\left ( \frac{n}{2} \right ): T\left ( \frac{n}{2} \right ) \leq c \frac{n}{2} \cdot log_{2}\frac{n}{2}\)
Induction step: prove that the inequality holds for the next step based on induction’s hypothesis.
Thus, it means that the inequality must hold for \(T(n)\):
\(T(n) \leq 2 \left ( c\frac{n}{2} \cdot log_{2}\frac{n}{2} \right ) + n\)
\(= cn \cdot log_{2}\frac{n}{2} + n\)
\(= cn \cdot log_{2}n - cn \cdot log_{2}2 + n\)
\(= cn \cdot log_{2}n + n(c - 1)\)
\(\leq cn \cdot log_{2}n\) – holds for \(c \geq 1\)
Conclusion: the inequality \(T(n) \leq cn \cdot log_{2}n\) holds for \(c \geq 2\) and all \(n > n_0 = 3\).
Master-Theorem
The theorem:
Let T(n) be a monotonically increasing function of the form \(T(n)=aT\left ( \frac{n}{b} \right )+f(n)\), where \(a \geq 1\) and \(b > 1\) are two constants, \(\frac{n}{b}\) is either \(\left \lfloor \frac{n}{b} \right \rfloor\) or \(\left \lceil \frac{n}{b} \right \rceil\) and \(f(n)\) is polynomial and asymptotically positive function (i.e. \(\exists m \in R^+\) such that \(f(n) > 0\) for \(\forall n > m\)). Then, the following statements are true:
- case 1: if \(f(n)= O\left ( n^{log_{a}b-\varepsilon } \right )\) for some constant \(\varepsilon > 0\), then \(T(n) = \Theta\left ( n^{log_{b}a} \right )\).
- case 2: if \(f(n)= O\left ( n^{log_{a}b} \right )\), then \(T(n) = \Theta\left ( n^{log_{b}a} \cdot log_{2}n \right )\).
- case 3: if \(f(n)= \Omega \left ( n^{log_{a}b+\varepsilon} \right )\) for some constant \(\varepsilon > 0\) and \(af\left ( \frac{n}{b} \right ) \leq cf(n)\) for some constant \(c > 1\) and all sufficiently large \(n\), then \(T(n) = \Theta\left ( f(n) \right )\).
For this algorithm, \(a\) and \(b\) are equal to \(2\), thus \(n^{log_{b}a} = n\), so the second case of the theorem is selected: \(T(n) = \Theta \left ( n^{log_{b}a} \cdot log_{2}n\right ) = \Theta\left ( nlog_{2}n \right )\).
Space Complexity (auxiliary)
At merge step the two halves are copied to two new arrays, so the auxiliary space complexity is \(S(n) = \Theta (n)\). If we count the stack frames, then we have \(T(n) = \Theta(n) + O(log_{2}n) = \Theta(n)\).
/ Back / Home /