/ Back / Home /
The Algorithm
Insertion sort is another simple sorting algorithm based on comparison, but unlike with the previous three, this one it is actually used. It maintains a sorted subsequence into which it inserts each item in its place, and thus produces the sorted sequence. The analogy I’ve seen most often is with the way people sort the playing cards.
Description
Lets assume that we have sorted the subsequence from index \(0\) to some index \(i-1 \lt n - 1\) and the subsequence from \(i\) to \(n - 1\) it is not. As the algorithm suggest, we need to insert all items from \(i\) to \(n - 1\) one by one into the sorted subsequence to their rightful place. The i-th item is inserted first by swapping it with all items to its left that are bigger then him. Then, the next item is inserted in the same way (basically, all items up to \(n - 1\) are inserted). See an example below:
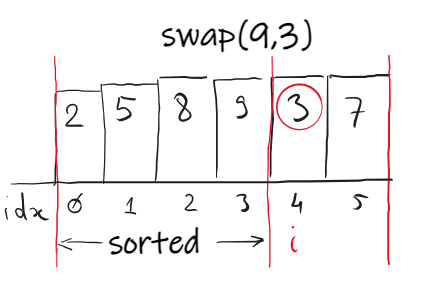
The i-th item (index 4, number 3) is inserted into the sorted subsequence (index 0 to 3).
There are 3 swaps until 3 is inserted between 2 and 5: (9,3), (8,3) and (5,3).
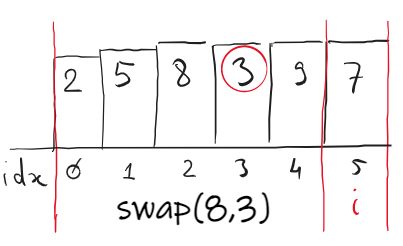
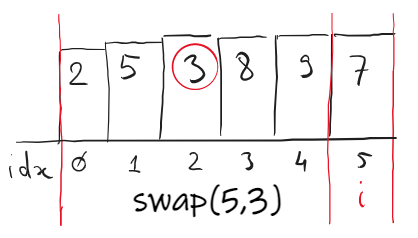
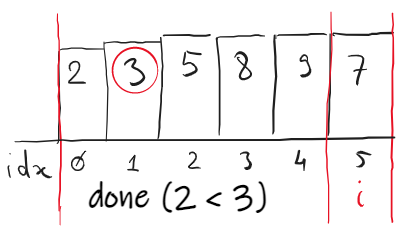
Implementation
void sort(vector<int> &a) {
if (a.size() <= 1) return;
for (int i = 1; i < (int)a.size(); ++i) {
for (int j = i; j > 0; --j) {
if (a[j - 1] > a[j]) swap(a[j], a[j - 1]);
else break;
}
}
}
Correctness
Initially, the sorted subsequence contains only the item from index \(0\) and the outter loop runs for all items starting with second index up to \(n - 1\), thus all items are inserted. The inner loop swap i-th item at most \(i - 1\) times and the subsequence is kept invariant. So, the algorithm sort any given input.
Complexity Analysis
Time Complexity
- Worst Case : \(\theta(n^2)\)
- Average Case : \(\theta(n^2)\)
- Best Case: \(\theta(n)\)
In the worst-case, the given sequence is sorted in opposite way, therefore the inner loop runs i times for each item.
\(T(n) = \sum_{i = 1}^{n-1} \left(\theta(i) \right) =\theta\left(\frac{n(n-1)}{2} \right) = \theta(n ^ 2)\).
In the average-case, each item is inserted in the middle of the sorted sequence, thus only half of the sequence is moved, or in other words, the inner loop runs \(\frac{i}{2}\) times for each item.
\(T(n) = \sum_{i = 1}^{n-1} \left(\theta\left( \frac{i}{2} \right) \right) =\theta\left(\frac{n(n-1)}{4} \right) = \theta(n ^ 2)\).
In the best-case, the given sequence is sorted, so the inner loop runs only 1 time.
\(T(n) = \sum_{i = 1}^{n-1} \left( \theta(1) \right) = \theta(n)\).
Space Complexity (auxiliary)
- \(S(n) = \theta(1)\).
/ Back / Home /