Graph traversals (or graph search) refers to the methods of visiting (and/or updating) the vertices of a graph. Depending on how the vertices are visited, we distinguish two methods: breadth first search (BFS) and depth first search (DFS). In the former method, the neighbors are visited first, while in the latter are the children.
Let’s assume we are at some vertex \(v\).
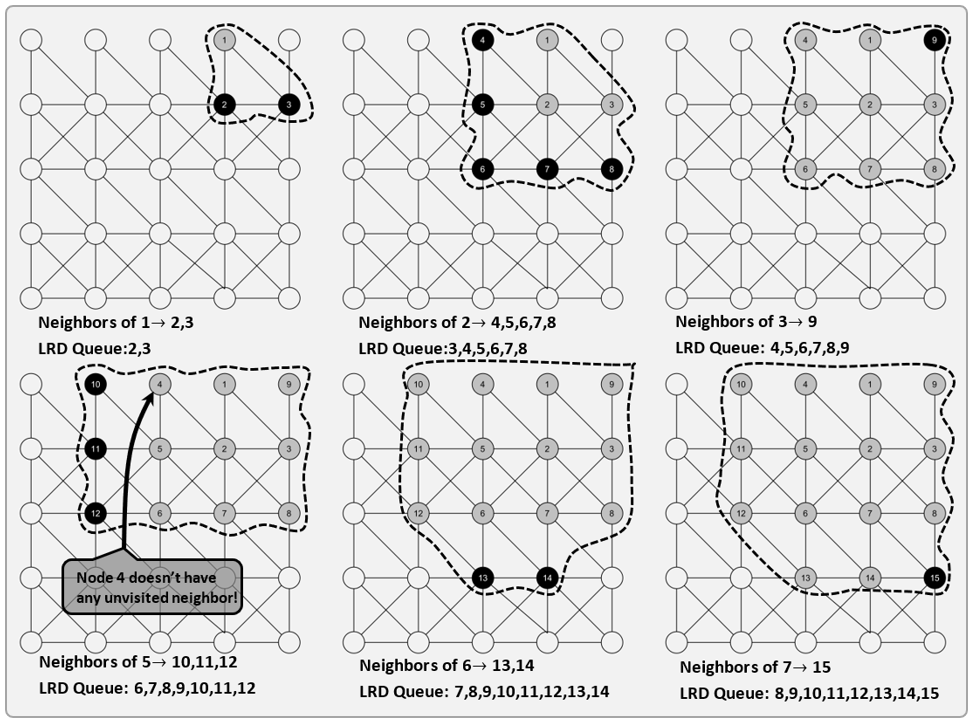
If we follow BFS method, we visit all its immediate neighbours (i.e. paths with no intermediate vertices / direct edges), then we take these vertices one by one and visit all their immediate neighbours. We continue this way until all of them are visited. Funny thing, I call this the plague method, because the border between visited and unvisited vertices grows like a plague.
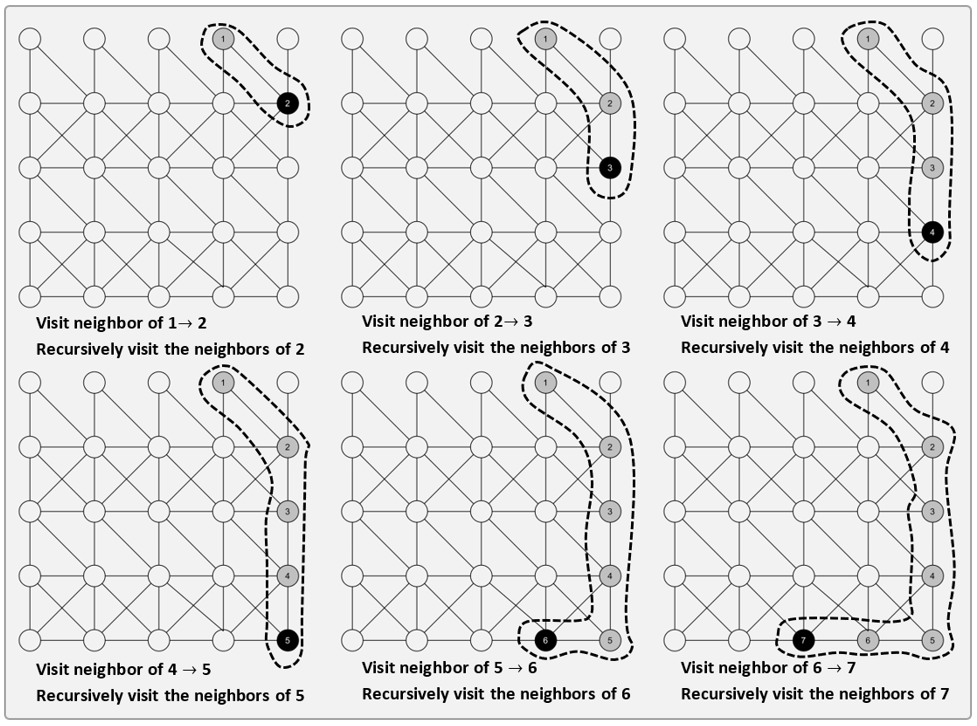
If we follow DFS method, then we visit one immediate neighbour of \(v\), and then continue with one immediate neighbour if this newly visited. Like for BFS, we continue this way until all vertices are visited. I call this the snake or the digger method, because we go as deeper as possible. DFS has the same profile as backtracking, because when there is nowhere to go deeper, we backtrack until we found some unvisited neighbour and again, we go deeper starting from this one.
For better understanding, see the pictures below:
Breadth First Search (BFS):
Depth First Search (DFS):
The Depth-first search algorithm
Description
Depth-First-Search (DFS) is one of the algorithms used to visit the nodes of a graph/digraph. DFS visits the children before the siblings, that is, before going in breadth, it visits the vertices in depth. Basically, it moves in depth until get stuck, then it backtracks and continue in depth from the first vertex that has at least one unvisited child. So, in essence, it uses the backtracking method.
For ease of understanding, let’s consider the recursive version. So, because in a recursion the last subproblem must be the first to finish, implies the use of a stack and a loop. Or a more accurate statement is that the LIFO principle of the stack is equivalent to the recursive calls in the sense that the earliest call is returned last. In this case, the stack is tracking the most recently discovered (MRD) vertex. In a loop, the vertices are popped from the top of the stack and all unvisited adjacent neighbours of any unvisited vertex are pushed into the stack. The algorithm ends when the stack is empty, meaning also that all reachable vertices were visited.
Implementations
The recursive version
vector<int> DFS::dfsr(int start, int n, vector<vector<int>>& adjL) {
vector<bool> marked(n, false);
vector<int> pred(n, - 1);
pred[start] = start;
dfsr(start, adjL, marked, pred);
return pred;
}
void DFS::dfsr(int u, vector<vector<int>>& adjL, vector<bool>& marked, vector<int>& pred) {
marked[u] = true;
for (int v : adjL[u]) {
if (marked[v] == false) {
pred[v] = u;
dfsr(v, adjL, marked, pred);
}
}
}
The iterative version
vector<int> DFS::dfsi_(int start, int n, vector<vector<int>>& adjL) {
if (adjL.empty()) return vector<int>();
vector<int> pred(n, -1);
vector<bool> marked(n, false);
vector<vector<int>::iterator> it(adjL.size());
for (int u = 0; u < n; u++) it[u] = adjL[u].begin();
stack<int> st;
st.push(start); marked[start] = true;
pred[start] = start;
while (!st.empty()) {
int u = st.top();
if (it[u] != adjL[u].end()) {
int v = *it[u]; it[u]++;
if (marked[v] == false) {
st.push(v); marked[v] = true;
pred[v] = u;
}
}
else st.pop();
}
return pred;
}
Complexity
Time Complexity
The time complexity for the iterative DFS method is similar to the one of BFS method. A vertex is visited at most once when it is popped from the stack. And just as for BFS, the adjacency list for each vertex is scanned once when a vertex is popped. So, the total running time of iterative DFS in the worst case is also \(T(V,E) = \theta \left ( V + E \right )\).
The recursive DFS visits each vertex at most once, since the recursive procedure is called if and only if the vertex wasn’t previously visited. In the same time, each adjacency list is scanned for each vertex when it is visited, thus it is scanned at most once. Same as before, the total time to visit all edges is \(O \left ( 2E \right )\), if the graph is undirected. So, the total running time of recursive DFS in the worst case is still \(T(V,E) = \theta \left ( V + E \right )\).
Space Complexity (auxiliary)
The auxiliary space complexity is obvious… the size of the stack can’t be bigger than the number of vertices, so \(S(V,E) = \theta \left ( V \right )\).
The Breadth-first search algorithm
TODO…