• Ford-Fulkerson
  • Complexity Issue
• Edmonds-Karp
  • Implementation

Ford-Fulkerson

Algorithm Steps:

• while an augmenting path from \(s\) to \(t\) exists in the residual network, augment the flow along the path
• update the residual network with every augment (along the path)
• return the maximal flow

Note: The interesting thing is that it doesn’t matter which path we choose to augment the flow, the algorithm finds the correct results anyway.

Complexity Issue

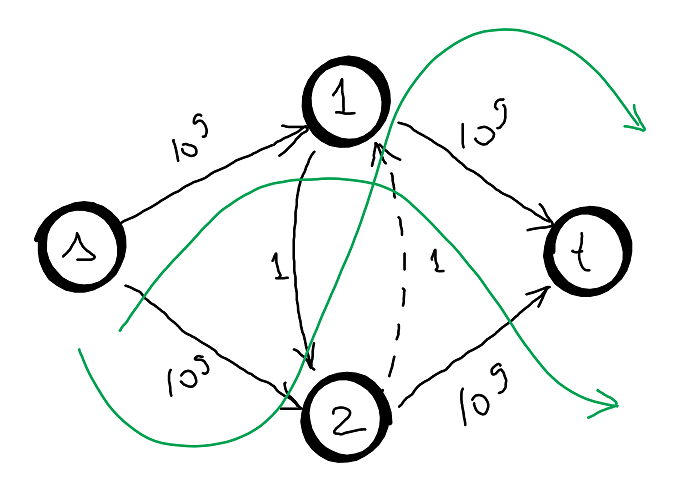
See the graph below. Each pass augments the flow by \(1\). In this example the middle edge is used by every augmenting path, then the complexity is bound by the maximum flow: \(T(V,E)=O((V+E) \cdot \left \| f_{max} \right \|) = O(E \cdot \left \| f_{max} \right \|)\).

Note: In case of irrational capacities, the Ford-Fulkerson is not guaranteed to finish, however Edmonds-Karp is. Edmonds-Karp is Ford-Fulkerson that uses BFS to find the augmenting paths. Its complexity is \(T(V,E) = O(VE^2)\) regardless of the capacities or graph profile.

Edmonds-Karp

Edmonds-Karp is basically Ford-Fulkerson that uses BFS (or any other algorithm that finds augmenting paths with minimal number of edges in \(G_f\)) instead of DFS. In which case there are \(O(VE)\) iterations instead of \(\left \| f_{max} \right \|\).

Intuition:
Every time an augmenting path is found, one of the edges become saturated, and the distance from the edge to \(s\) will be longer If it appears again in an augmenting path.
Since the length of the simple path from \(s\) to \(t\) is bound by \(V\), then an edge can appear at most \(V\) times in augmenting paths.
So, \(E\)-edges, each can appear \(V\) times \(\Rightarrow O(VE)\) iterations, so: \(T(V,E) = O((V+E)VE) = O(V^2)\).

Proof:

1. The shortest path from \(s\) to \(t\) increases monotonically in \(G_f\). A note: the shortest path in this case is the number of edges.
2. If (1) then the total number of augmentations in \(G_f\) is \(O(VE)\).

1. Monotonically Increasing:
Consider flow \(f\) before augmentation with the shortest path that decreases.
Consider flow \(f^{’}\) after augmentation with the shortest path that decreases.
This implies that there is a node \(v\) such that \(d_{f^{‘}} (s,v) < d_f(s,v)\), where \(d_f\) is the distance in \(G_f\) and \(d_{f^{‘}}\) is the distance in \(G_{f^{‘}}\).
Let the shortest path in in \(G_{f^{‘}}\) from \(s\) to \(t\) be through \(u\) and for simplicity, let’s say \((u,v) \in E_{f^{‘}}\) so that \(d_{f^{‘}} (s,u) = d_{f^{‘}} (s,u) -1\) (1)
The shortest path from \(s\) to \(u\) did not decrease with \(f^{‘}\) because of how we chose \(v\), so \(d_{f^{‘}} (s,u) \geq d_{f^{‘}} (s,u)\).
However, the edge \((u,v)\) cannot be in \(G_f\), because if it were, then we would have:
\(d_f(s, v) \leq d_f(s,u) + 1\) (triangle inequality)
\(d_f(s,v) \leq d_{f^{‘}} (s,u) + 1\) (because the shortest path decreases with \(f^{‘}\))
\(d_f(s,v) \leq d_{f^{‘}} (s,v) - 1 + 1\) - contradicts the assumption that \(d_{f^{‘}} (s,v) < d_f(s,v)\)
So, the shortest path did not decrease with flow \(f^{‘}\).

2. Number of iterations:
A critical edge is the edge with the least weight in an augmenting path. We need to prove that an edge can be critical at most \(V/2\) times.
Let \((u,v)\) be such a critical edge, then: \(d_f(s, v) = d(s,u) +1\)
Once the flow is augmented, the critical edge \((u,v)\) disappear from the residual network and it can only reappear if the flow on \((u,v)\) decreases , which only happens if the edge \((v,u)\) appears on the augmenting path. Let \(f^{‘}\) be the flow when this happens, then:

• \(d_{f^{‘}}(s,u) = d_{f^{‘}}(s, v) + 1\).
• \(d_f(s,v) \leq d_{f^{‘}}(s, v)\) ( from (1) when we showed that the distance can only increases)
• From \(d_{f^{‘}}(s,u) = d_{f^{‘}}(s,v) + 1\) and \(d_{f^{‘}}(s,u) \geq d_{f}(s,v) + 1\) implies \(d_{f^{‘}}(s,v) \geq d_{f}(s,v) + 1\)
• \(d_{f^{‘}}(s,u) \geq d_{f}(s,u) + 2\) (since \(d_{f}(s,v) \geq d_{f}(s,u) + 1\)) – this means that between the time \((u,v)\) first become critical and second time, the distance between the source and \(u\) increases by at least \(2\).

The intermediate nodes on the shortest path from \(s\) to \(u\) connot contain \(s\), \(u\) or \(t\), thus the distance from \(s\) to \(u\) can be at ost \(V-2\).
Since the distance increases by at least \(2\) every time an edge become critical again, the denomination is \(2\).
So, \((u,v)\) can become critical \(\frac{V-2}{2}\) times for a total of \(O(V)\).
Since there are \(E\) edges (or \(E\) pairs of nodes) the total number of critical edges is \(O(VE)\).
So, \(T(V,E)=O((V+E)VE) = O(VE^2)\)
q.e.d

Implementation

// Edmonds-Karp
int maxflow_(int s, int t, vector<vector<int>>& adjM) {
	int n = adjM.size();
	vector<int> path(n, -1);
	int max_flow = 0;

	int cfp = find_path(s, t, adjM, path);   // find augmenting path in residual network
	while (cfp > 0) {                        // if there is such path with residual capacity > 0
		max_flow += cfp;
		augment_flow(s, t, cfp, adjM, path); // augment flow along the path
		cfp = find_path(s, t, adjM, path);   // find another augmenting path
	}

	return max_flow;
}

// Find an augmenting path from s to t (i.e. BFS: the shortest) and return its residual capacity
int find_path(int s, int t, vector<vector<int>>& adjM, vector<int>& path) {
	int n = adjM.size();
	fill(path.begin(), path.end(), -1);

	int cfp = INF;
	queue<pair<int, int>> q;
	q.push({ s, cfp }); path[s] = 0;
	while (!q.empty()) {
		int u = q.front().first;
		cfp = q.front().second;
		q.pop();

		if (u == t) break;

		for (int v = 0; v < n; v++) {
			if (path[v] != -1) continue;
			if (adjM[u][v] == 0) continue;

			int new_cfp = min(cfp, adjM[u][v]);
			q.push({ v, new_cfp }); path[v] = u;
		}
	}

	if (path[t] == -1) return 0; // no augmenting path available
	return cfp;
}

// Augment the flow along the given path
void augment_flow(int s, int t, int cfp, vector<vector<int>>& adjM, vector<int>& path) {
	int v = t;
	while (v != s) {
		int u = path[v];

		adjM[u][v] -= cfp;
		adjM[v][u] += cfp;

		v = u;
	}
}