Define the Problem

Definition: Flow Network is a quadruple \(N=(G,S,t, c)\), where:

  • \(G=(V,E)\) is a digraph with the constraint that if \((u,v) \in E\), then \((v,u) \not \in E\)
  • \(s, t \in V\) are distinct nodes named source and sink
  • \(c: E \rightarrow R^{+}\) is a capacity function


The problem: What is the maximum flow from node \(s\) to node \(t\) ?
Intuition: If edges are tubes with capacity \(c\), then what is the maximum amount of water that can flow from \(s\) to \(t\).


Definition: A flow is a function \(f:V \times V \rightarrow R^{+}\) with the following properties:

  • the capacity constraint: \(0 \leq f(u,v) \leq c(u,c)\) for any \(u, v \in V\)
  • the conservation property: for any \(u, v \in V \setminus \left \{ s, t \right \}\), \(\sum_{v \in V} f(v,u) = \sum_{v \in V} f(u, v)\)


Definition: The value of a flow is defined by the amount of the flow passing from source to sink: \(\left \| f \right \| = \sum_{v \in V} f(s,v)\)


Definition: The residual network is the flow network \(N_f=(G_f, S, t, c_f)\) induced by flow \(f\). The capacity function \(c_f\) is the capacity induced by \(f\), defined by:
\(c_f(u,v) = \begin{cases} c(u,v)-f(u,v) & \text{if } (u,v) \in E \\ f(v, u) & \text{if } (v,u) \in E \\ 0 & \text{otherwise } \end{cases} \quad\)


Definition: An augmenting path is any simple path form \(s\) to \(t\) in the residual network. The augmenting path has the capacity defined as:
\(c_f(p) = min \left \{ c_f(u,v) \text{ : } (u,v) \in p \right \}\)


Definition: A CUT is a partition of nodes into \(2\) disjoint sets \(S\) and \(T\), such that \(s \in S\) and \(t \in T\). In this context we define:

  • The capacity of the CUT: \(\left \| S,T \right \| = \sum_{u \in S, v \in T} c(u,v))\)
  • The flow across the CUT: \(f(S,T)= \sum_{u \in S, v \in T} f(u,v) - \sum_{u \in S, v \in T} f(v,u)\)


The Max-Flow Min-Cut theorem: The maximum flow in a given flow network is equal to the maximum capacity over all \(S,T\) cuts.


Intuition:
The flow of a cut is less or equal to the capacity of the cut, because of the capacity constraint of the flow definition. This basically means that the maximum flow is less or equal to the capacity of every cut in the flow network.
Let’s assume there is no augmenting path from \(s\) to \(t\). Let set \(S\) contain all nodes reachable from \(s\) through a non-full direct edge and let set \(T\) contain all the other nodes.
Every edge that has its start-point in \(S\) and the endpoint in \(T\) has flow equal to its capacity. Every edge that has its start-point in \(T\) and the endpoint in \(S\) has flow equal to \(0\), otherwise this edge would have had its start-point in \(S\). Thus, the value of the flow must be equal to the capacity of the CUT. This must be maximal since every flow is less or equal to every CUT, and the CUT must be minimal as well.
Also, we can observer that when flow is maximal, there is no path from \(s\) to \(t\) and the min-cut disconnects \(s\) from \(t\).

pic_01

Proof:

  1. prove that for any \(\left \| f \right \| \leq \left \| S,T \right \|\)
  2. if \(t\) is not reachable from \(s\) in \(G_f \Rightarrow f \text { is maximum }\)
    From (1) and (2) \(\Rightarrow \left \| f \right \| = min \left \| S,T \right \|\)


1. \(\left \| f \right \| = \sum_{x \in V} f(s, x) - \sum_{y \in V} f(y, x)\) - by definition
Let \(S,T\) be a CUT in \(G\) then \(\sum_{v \in S} \left ( \sum_{x \in V} f(v, x) - \sum_{y \in V} f(y, v) \right ) =\)
\(= \sum_{v \in S} \left ( \sum_{x \in S} f(v, x) - \sum_{y \in S} f(y, v) \right ) + \sum_{v \in S} \left ( \sum_{x \in T} f(v, x) - \sum_{y \in T} f(y, v) \right ) =\)
The first term is \(0\) because each edge from a node appears twice since we sum over all nodes in \(S\). \(= \sum_{v \in S} \left ( \sum_{x \in T} f(v, x) - \sum_{y \in T} f(y, v) \right ) \leq \sum_{v \in S}\sum_{x \in T} f(v,x) \leq \sum_{v \in S}\sum_{x \in T} c(v,x) = \left \| S,T \right \|\) \


2. Let a CUT \(S,T\) in the original \(G\), where \(S\) is the set of nodes reachable from \(s\) in \(G_f\), and \(T\) is the set of nodes that are not. Observe that there are no edges between the nodes in \(S\) and nodes in \(T\) in \(G_f\), otherwise one of the nodes in \(T\) would be reachable from \(s\). So, for all \(u \in S\), \(v \in T\), we have \(c_f(u,v)=0\).

There are 3 cases:
a. if \((u,v)\) is an edge in original graph, then \(c_f(u,v)=c(u,c)-f(u,v)=0\)
b. if \((v,u)\) is an edge in original graph, then \(c_f(u,v)=f(v,u)=0\)
c. otherwise it doesn’t matter because the edge does not appear in any flow or cut.
From (1) we have \(\left \| f \right \| = \sum_{u \in S} \left ( \sum_{x \in T} f(x, u) - \sum_{y \in T} f(u, y) \right ) = \sum_{u \in S} \left ( \sum_{x \in T} c(u, x) - \sum_{y \in T} 0 \right ) = \left \| S,T \right \| \Rightarrow f\) must be maximum since it is equal to the cut through capacity constraints.


Theorem: If there is a path in \(G_f\) then we can augment the path in \(G\).


Proof: Let \(p = X_0 \rightarrow x_1 … \rightarrow x_k\), where \(x_0 = s\) and \(x_k = t\) in \(G_f\).
Let \(\alpha = min_{i} \left \{ c_f (x_i, x_{i+1}) \right \}\)
We may increase the flow \(f\) in \(G\) by augmenting it by \(\alpha\). \

  • if there is an edge \(x_i \rightarrow x_{i+1}\) in original graph, then \(f + \alpha\) on that edge
  • if there is an edge \(x_{i+1} \rightarrow x_i\) in original graph, then \(f - \alpha\) on that edge


We can always do this in \(G_f\) because of the capacity constraints:
\(f^{‘}(u,v) = \begin{cases} f(u, v) + \alpha & \text{if } (u,v) \in p \\ f(v, u) - \alpha & \text{if } (v,u) \in p \\ f(u,v) & \text{otherwise } \end{cases} \quad\)


We need to prove that \(f^{‘}\) obeys the capacity constraints and has the conservation property, also \(f^{‘} > f\).

  1. capacity constraint:
    (1) if \((u,v) \in p\) then \(0 \leq f(u,v) + \alpha \leq f(u,v) + c_f(u,v) = f (u,v) + c(u,v) – f(u,v) = c(u,v) \Rightarrow 0 \leq f^{‘}(u,v)=f(u,v) + \alpha \leq c(u,v)\)
    (2) if \((v,u) \in p\) then \(f(u,v) - \alpha \leq f(u,v) \leq c(u,v)\) and \(f(u,v) - \alpha \geq f(u,v) – c_f(u,v) = 0\), so that means \(0 \leq f(u,v) - \alpha \leq f(u,v)\)
    (3) otherwise \(f^{'}(u, v) = f(u,v)\)

  2. conservation constraint:
    For any \(v \in V \setminus {s, t}\), if \(v\) touches either \(0\) or \(2\) edges in \(p\). In the first case the flow is conserved, in second case we need to prove.
    Case 1: \(f(x,v) + \alpha + \sum_{x^{‘} \neq x}f(x^{‘},v) = f(v,y) + \alpha + \sum_{y^{‘} \neq y}f(v, y^{‘})\) – conserved
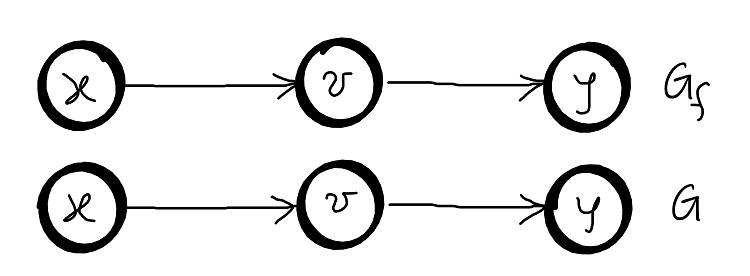
    pic_02
    Case 2: \(f(x,v) - \alpha + \sum_{x^{‘} \neq x}f(x^{‘},v) = f(v,y) - \alpha + \sum_{y^{‘} \neq y}f(v, y^{‘})\) – conserved
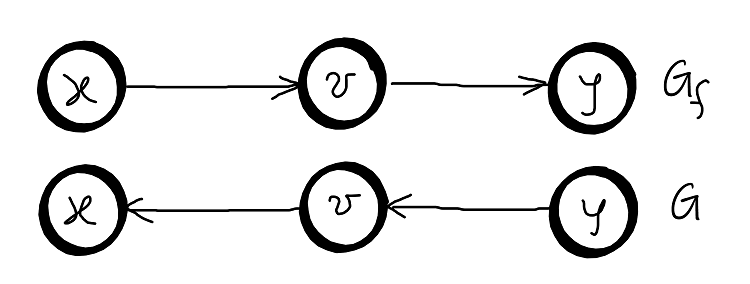
    pic_03
    Case 3: \(\sum_{z^{‘} \in V }f(v, z^{‘}) = f(x, v) + \alpha + f(y, v) - \alpha + \sum_{z \neq x, z \neq y}f(v, z)\) – conserved
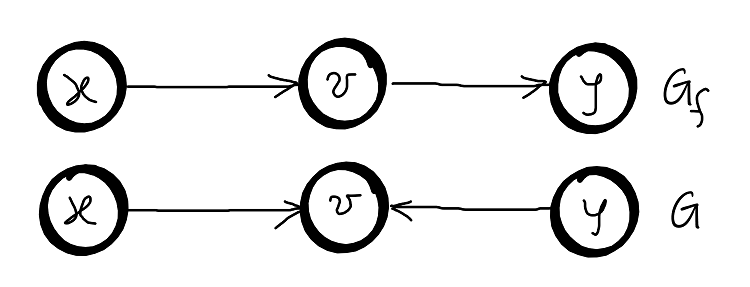
    pic_04
    Case 4: \(f(v,x) - \alpha + f(v,y) + \alpha + \sum_{z \neq x, z \neq y}f(v, z) = \sum_{z^{‘} \in V }f(z^{‘}, v)\) – conserved
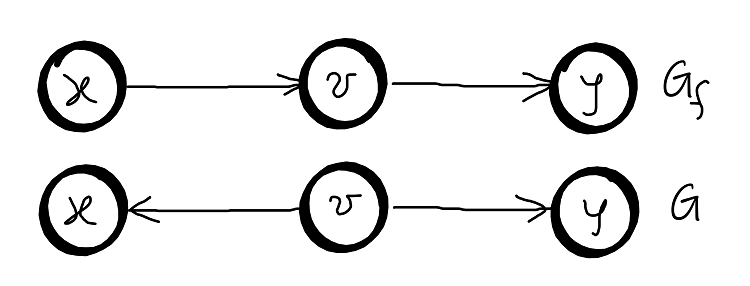
    pic_04
    From 1, 2, 3, and 4 \(\Rightarrow f^{'}\) is conserved. And, \(\left \| f^{'} \right \| > \left \| f \right \|\) because \(\alpha > 0\).
    q.e.d.


Find the min-cut, max-flow:



Learning resources: