Definitions
A graph is a classic method of modeling relationships between the items/locations of a collection. This type of structure is used in many areas, such as the roads system, computer networks, social networks, software programs (classes interactions) and so on.
By modeling problems this way, we can answer questions like:
- Is there a relation between a subset of given locations?
- If the relations have costs (e.g. distance between cities), what is the minimum cost that connects all or a subset of given locations?
- Are all locations connected? Which locations forms connected groups?
- Let’s assume that these relations between locations represents bandwidth, then how much cargo can be transported between two given locations?
Of course, this is just a very small subset of questions, there are many other that we can answer using graph algorithms.
Before jumping to the algorithms, let’s define the following notions: graph, edge, vertex, adjacent vertices, incident edges, the degree of a vertex, path, and cycle, as well as several methods of graphs representation: adjacency list, adjacency matrix and incidence matrix.
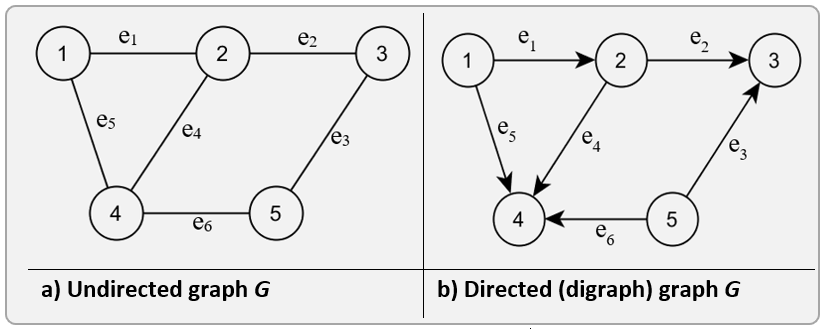
Def: A graph is an abstract data structure that shapes the relationships among the items of a collection. Representing the items as vertices and the relationships among them as edges, a graph is expressed as a pair
\(G = (V, E)\), where \(V = \{v_0, v_1, ... , v_n \}\) is a finite set of vertices and \(E = \{e_0, e_1, ... , e_n \}\) is a finite set of edges. The size of the graph
\(G\) is given by the number of edges \(m = \left \| E \right \|\) and the order by the number of vertices \(n = \left \| V \right \|\). An edge \(e \in E\) is a pair of vertices \((v_i, v_j)\), where, \(v_i, v_j \in V\). If all pairs that shape the edges of a graph are unordered, then the graph is called undirected. Otherwise, if all are ordered then the graph is called directed or digraph.
Immediate definitions:
- Let \(u, v ∈ V\) be two vertices from a graph \(G = (V, E)\). The vertices \(u\) and \(v\) are adjacent if they are connected by an edge \(e \in E\), denoted as: \(( u ~ v )\).
- Let \(e \in E\) be an edge from a graph \(𝑮 = (𝑽, 𝑬)\). The edge \(e\) is incident to the vertex \(v \in V\) if the vertex \(v\) is one endpoint of the edge \(e\), denoted as: \(( v \in e )\).
- Let \(v \in V\) be a vertex from a graph \(𝑮 = (𝑽, 𝑬)\). The degree of the vertex \(v\) is the number of edges incident to it, denoted as: \(deg (𝒗)\).
Def: Given an undirected graph \(G = (V, E)\), a path \(u\overset{p}{\rightarrow}v\) from vertex \(u \in V\) to vertex \(v \in V\) is a sequence of vertices \(p = (v_0, v_1, ... , v_k )\), where \(u = v_0\), \(v = v_k\), and \(( v_i. v_{i+1} )\in E\) for \(i = 1\) to \(k-1\). The length of the path \(p\) is given by the number of edges that make up the path.
-
If graph \(𝑮 = (𝑽, 𝑬)\) is directed (digraph), all edges in the path must be directed in the same direction (in this case sometimes, the path is called directed path or dipath).
-
A simple path is a path which contains no repeated vertices (i.e. no cycles).
Def: A cycle is a path where the vertices in the path appear exactly once, except the first and the last vertex which coincide. Sometimes it is called circular path.
So, a tree can be defined as an acyclic graph.
Representations
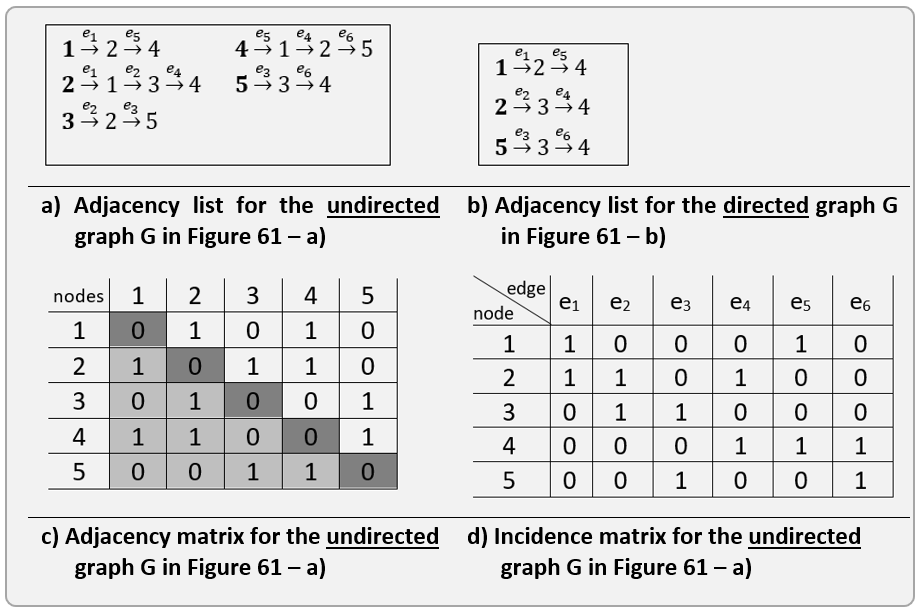
- Adjacency list:
- Def: The adjacency list for a graph \(G\) is the set of lists \(\{ L_i \vdots i = 1, n \text{ where } n = \left\| V \right\| \}\), for a graph \(G\) is the set of lists \(\{ L_i \vdots i=1,n \text{ where } n = \left\| V \right\| \}\), where each list \(L_i\) is the set of neighbors of vertex \(v_i\), defined as \(L_i = \{ v_j \vdots v_j~v_i, \text{ where } v_j \in V \}\).
- This representation is better suited for sparse graphs, which means: \(\left \| E \right \| << \left \| V \right \|^{2}\)
- Space complexity is \(\theta (E + V)\)
- Adjacency matrix:
- Def: The adjacency matrix for a graph \(G\) is defined as: \(A_{nxn} = (a_{ij}), \text{ where } a_{ij} = \left\{ \begin{matrix} 1 \text{ if } (ij) \in E\\ 0 \text{ otherwise } \end{matrix}\right.\)
- This representation is better suited for dense graphs, which means: \(\left \| E \right \| \sim \left \| V \right \|^{2}\)
- Space complexity is \(\theta (\left \| V \right \|^{2})\). If \(G\) is an undirected graph, then \(A = A^{T}\), hence only half of the matrix must be stored.
- Incidence matrix:
- Def: The incidence matrix for a graph \mathbit{G} is defined as: \(A_{nxm} = (a_{ij}), \text{ where } a_{ij} = \left\{ \begin{matrix} 1 \text{ if } v_i \in e_j\\ 0 \text{ otherwise } \end{matrix}\right.\)
- Space complexity is \(\theta (VE)\)