- Defining the Problem
- Hamiltonian Path (Bellman-Held-Karp)
- Hamiltonian Cycle (Bellman-Held-Karp)
- Traveling Salesman Problem (Bellman-Held-Karp)
Defining the Problem
Hamiltonian path is a path in a graph/digraph that visit each node exactly once.
Hamiltonian cycle is a Hamiltonian path for which the start node and end node coincide.
The Hamiltonian path/cycle problems are the problems of determine whether such a path/cycle exists in a given graph/digraph.
Traveling Salesman Problem is the problem of finding the shortest Hamiltonian Cycle in a given weighted graph/digraph (if such a cycle exists).
Complexity Class Classification of Hamiltonian Problems
First, complexity class classification in practice:
- The solutions to P problems are fast (i.e. for some constant \(c\) the time complexity is in form of \(O(n^c)\))
- The solutions to NP problems are slow, but fast to verify (i.e. only the verification is in polynomial time)
- The solutions to NP Complete problems are slow, but fast to verify and all NP problems can be reduced to it
- The solutions to NP Hard problems are slow and also slow to verify and all NP problems can be reduced to it
Hamiltonian Path/Cycle is NP-Complete, because it is NP (since we can verify its solution in polynomial time, but we cannot find the cycle in polynomial time) and it is also NP-Hard, but proving it is NP-Hard is not trivial.
Travelling Salesman Problem is NP-Hard since we cannot verify the shortest Hamiltonian Cycle in polynomial time, basically we need to find all Hamiltonian cycles to know which one is the shortest.
Approaches
Brute force: Enumerate all permutations of all \(n\) nodes and for each permutation verify if it is Hamiltonian path/cycle. Stop when found. The time complexity in the worst case is \(O(n!)\).
Backtracking: Is no better than brute force in the worst case, however in practice is faster.
Bellman-Held-Karp: Is a dynamic programming approach (discussed further) and its running time is \(O(n^2 \cdot 2^n)\). This approach is definitely better than brute force and backtracking, but still intractable (i.e. \(k^n, n!, n^n\)).
Note: There are also approached that gives an approximated solution with a specific probability such us Simulating Annealing or Genetic Algorithms.
Hamiltonian Path (Bellman-Held-Karp)
The basic idea: Suppose that you are walking along a path in a graph, and you try to construct a Hamiltonian path. After you visited some nodes, you don’t need to remember the actual order of nodes you just visited, you just need to remember the set of nodes you visited to construct the Hamiltonian path.
Formally, we construct a table \([2^n] x [n]\) such that \(T(S,v) = 1\) iff there is a path that visits exactly the nodes in \(S\) and ends with node \(v \in S\). So, the dynamic programming table is defined as:
\(d[k][mask]=\begin{cases}
1 & \text{if there is a path that visits all nodes in mask and ends with k } \\
0 & \text{otherwise}
\end{cases}\)
Note: The masks form a DAG (Direct Acyclic Graph), because the binary numbers are constructed incrementally.
Base case: \(dp[k][2^k] = 1\) - the set that contains only node \(k\) and ending with \(k\)
General case: \(dp[k][mask] = 1\) if \(dp[j][ mask \setminus \left \{ k \right \}] = 1\) and \(a[j][k] == 1\) (i.e. there is an edge from j to k), for all \(j \in mask \setminus \left \{ k \right \}\) and \((j,k) \in E\).
The \(mask \setminus \left \{ k \right \}\) is the set chosen by mask less node \(k\): \(mask \oplus 2^k\).
Hamiltonian Path exists iff \(dp[k][2^n-1] == 1\) for some k.
Implementation
vector<int> hamiltonianPath(int n, vector<vector<bool>>& adjM) {
int all = (1 << n) - 1; // 2^n - 1 = 111...1
vector<vector<bool>> dp(n, vector<bool>(all + 1, false));
vector<vector<int>> pred(n, vector<int>(all + 1, -1));
// initialize the dp and predecessor tables
for (int k = 0; k < n; k++) {
dp[k][1 << k] = true;
pred[k][1 << k] = k;
}
for (int mask = 3; mask <= all; mask++) { // mask = current set of vertices
for (int k = 0; k < n; k++) {
if (((1 << k) & mask) == 0) continue; // if vertex k is not in the set
int mask_nok = mask ^ (1 << k); // the set-{k}
for (int j = 0; j < n; j++) {
if (((1 << j) & mask_nok) == 0) continue; // if vertex j is not in the set-{k}
if (dp[j][mask_nok] && adjM[j][k]) {
dp[k][mask] = true; pred[k][mask] = j;
break;
}
}
}
}
int s = -1;
for (int k = 0; k < n; k++) {
if (dp[k][all] == true) {
s = k;
break;
}
}
if (s == -1) return vector<int>(0);
return build_path(s, n, pred);
}
Hamiltonian Cycle (Bellman-Held-Karp)
Any Hamiltonian Cycle must contain all vertices and must be a closed path. So, we can choose the path that closes in node \(0\). Thus, we remove node \(0\) from the set and initialize the dp table for the other nodes with \(1\) if there is a path from \(0\), otherwise with \(0\). After we compute all Hamiltonian paths for the set (less \(0\)), we check if any of the ending nodes has also an edge to node \(0\) (i.e. a close path = cycle).
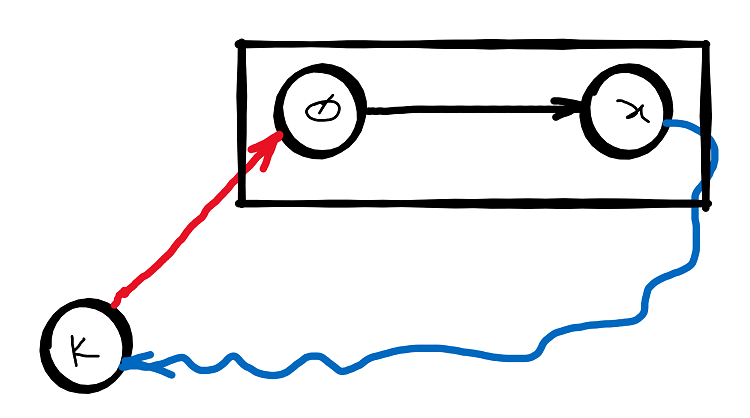
Since only nodes \(x\) with edge from \(0\) has been enabled and we know that we have a Hamiltonian path from \(x\) to some node \(k\) then if there is an edge from \(k\) to \(0\) it means we found a Hamiltonian cycle.
Implementation
vector<int> hamiltonianCycle(int n, vector<vector<bool>>& adjM) {
int all = (1 << n) - 1; // 2^n - 1 = 111...1
vector<vector<bool>> dp(n, vector<bool>(all + 1, false));
vector<vector<int>> pred(n, vector<int>(all + 1, -1));
// initialize the dp and predecessor tables
for (int k = 0; k < n; k++) {
if (adjM[0][k]) { // there is an edge from vertex 0 to k
dp[k][1 << k] = true;
pred[k][1 << k] = 0;
}
}
for (int mask = 3; mask <= all; mask++) { // mask = current set of vertices
if (mask & 1) continue; // vertex 0 removed from the set
for (int k = 1; k < n; k++) {
if (((1 << k) & mask) == 0) continue; // if vertex k is not in the set
int mask_nok = mask ^ (1 << k); // the set-{k}
for (int j = 1; j < n; j++) {
if (((1 << j) & mask_nok) == 0) continue; // if vertex j is not in the set-{k}
if (dp[j][mask_nok] && adjM[j][k]) {
dp[k][mask] = true; pred[k][mask] = j;
break;
}
}
}
}
// close the cycle by adding the edge k -> 0
for (int k = 1; k < n; k++) {
if (dp[k][all - 1] && adjM[k][0]) {
dp[0][all] = true;
pred[0][all] = k;
break;
}
}
if (pred[0][all] == -1) return vector<int>(0);
return build_cycle(0, n, pred);
}
Traveling Salesman Problem (Bellman-Held-Karp)
The idea is similar with Hamiltonian Cycle: choose the path that closes to node \(0\), so we remove node \(0\) from the set and initialize the dp table for the other nodes with the value \(a[0][k]\) if there is a path from \(0\) to \(k\), or \(INF\) otherwise.
When the path is constructed, instead break after the first path, continue and minimize over all paths.
After all shortest Hamiltonian Paths for the set (less \({0}\)) has been found, we check if any of the ending nodes has also an edge to node \(0\), and store the shortest cycle (i.e. TSP).
Implementation
vector<int> TSP(int n, vector<vector<int>>& adjM) {
int all = (1 << n) - 1; // 2^n - 1 = 111...1
vector<vector<int>> dp(n, vector<int>(all + 1, INF));
vector<vector<int>> pred(n, vector<int>(all + 1, -1));
// initialize the dp and predecessor tables
for (int k = 0; k < n; k++) {
if (adjM[0][k] != INF) { // there is an edge from vertex 0 to k
dp[k][1 << k] = adjM[0][k];
pred[k][1 << k] = 0;
}
}
for (int mask = 3; mask <= all; mask++) { // mask = current set of vertices
if (mask & 1) continue; // vertex 0 removed from the set
for (int k = 1; k < n; k++) {
if (((1 << k) & mask) == 0) continue; // if vertex k is not in the set
int mask_nok = mask ^ (1 << k); // the set-{k}
for (int j = 1; j < n; j++) {
if (((1 << j) & mask_nok) == 0) continue; // if vertex j is not in the set-{k}
if (dp[j][mask_nok] == INF) continue; // no path from 0 to j
if (adjM[j][k] == INF) continue; // no edge from j to k
if (dp[k][mask] > dp[j][mask_nok] + adjM[j][k]) { // minimize (relax)
dp[k][mask] = dp[j][mask_nok] + adjM[j][k];
pred[k][mask] = j;
}
}
}
}
// close the cycle by adding the edge k -> 0
for (int k = 1; k < n; k++) {
if (dp[k][all - 1] == INF) continue;
if (adjM[k][0] == INF) continue;
if (dp[0][all] > dp[k][all - 1] + adjM[k][0]) {
dp[0][all] = dp[k][all - 1] + adjM[k][0];
pred[0][all] = k;
}
}
if (pred[0][all] == -1) return vector<int>(0);
return build_cycle(0, n, pred);
}