Algorithm
A simple cycle in a weighted graph/digraph is a path that contains no repeated nodes except the first node with coincide with the last node. The simple shortest cycle (girth) in a graph/digraph is the simple cycle that uses the smallest number of edges and in a weighted graph/digraph is the cycle with the smallest weight.
One solution is to remove each edge and find the shortest path between its endpoints and then add that last edge to the path and form the cycle. The answer is the shortest cycle among all the cycles found this way. A more elegant solution is to use Floyd-Warshall. The weights of all the cycles are on the diagonal of the dp table so, the shortest will have the smallest value.
- Breadth-First Search: \(T(V, E) = O(E \cdot T_{BFS}) = O(E(V+E))\)
- \(T(V, E) = O(V^4)\) - dense graphs (\(E ~ V^2\))
- \(T(V, E) = O(V^2)\) - sparse graphs (\(E ~ V\))
- Dijkstra: \(T(V, E) = O(E \cdot T_{Dijkstra}) = O(E(V+E)log(V))\)
- \(T(V, E) = O(V^4log(V))\) - dense graphs (\(E ~ V^2\))
- \(T(V, E) = O(V^2log(V))\) - sparse graphs (\(E ~ V\))
- Floyd-Warshall: \(T(V, E) = O(V^3)\)
Note: The algorithms can be found in the following sections:
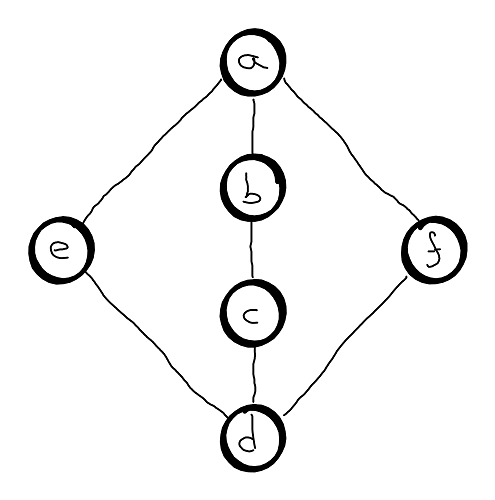
Pitfall
You may be tempted to apply DFS level to compute the shortest cycle, but it won’t work, see the example below. So, if the path \(a, b, c, d\) is visited first then the shortest path is never found (i.e. \(a, f, d, e, a\)) .