• Algorithm
• Correctness
• Implementation
• Complexity

Algorithm

Plain Dijkstra: \(T(V,E) = O((V+E)log(V))\)

• dense graphs \(E = V^2 \Rightarrow T(V,E) = O(V^2log(V))\)
• sparse graphs \(E ~ V^2 \Rightarrow T(V,E) = O(Vlog(V))\)

Running Dijkstra for all nodes we get:

• dense graphs \(E = V^2 \Rightarrow T(V,E) = O(V^3log(V))\)
• sparse graphs \(E ~ V^2 \Rightarrow T(V,E) = O(V^2log(V))\)

For sparse graphs Dijkstra is faster than Floyd-Warshall: \(O(V^2log(V)) < O(V^3)\).
Johnson’s algorithm uses Dijkstra, but since Dijkstra works only with non-negative weights we need a method to make all weights positive. One way would be to find the shortest edge and add it to all the other edges and then subtract it from the shortest paths. But, this method doesn’t work in all cases since there maybe multiple paths from (let’s say) node \(s \rightarrow v\) and all these paths should increase with the same amount to preserve the shortest path, see the graph below.

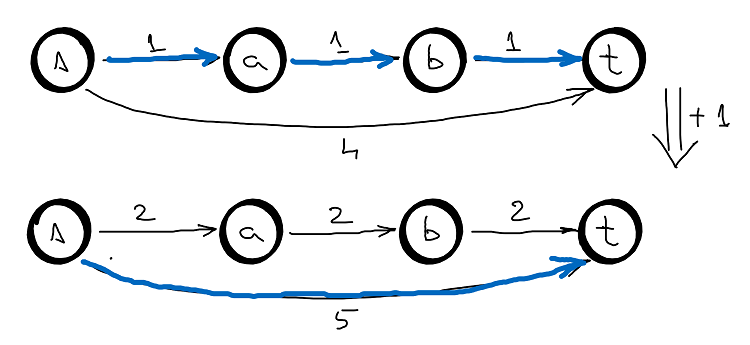
So, Johnson’s algorithm have the following idea: reweight every node so that \(w(u,v) + h(u) -h(v) \geq 0\).
Johnson’s algorithm main steps:

1. Find the function \(h:V \rightarrow R\) such that \(w_h(u,v) = w(u,v) + h(u) + h(v) \geq 0\) for all \(u,v \in V\) or determine that \(G\) has negative cycles.
2. Run Dijkstra on \(G_h=(V,E,w_h)\) for every node \(u \in V\) and find \(\delta_h(u,v)\) for all \(v \in V\).
3. Given \(\delta_h(u,v)\) and \(h\) compute \(\delta(u,v)\) for all \(u,v \in V\).

Correctness

Claim 1: Lets assume we know \(h:V \rightarrow R\) and we want to prove that the shortest path in \(G\) is the same with the shortest path in \(G_h\).

Basically, we claim that \(\delta(u,v) = \delta_h(u,v) - h(u) + h(v)\).
Let \(p: v_0 \rightarrow v_1 \rightarrow v_2 \rightarrow ... \rightarrow v_k\) is the path \(v \rightarrow u\) and \(v_0 = u, v-k = v\).
\(w_h(p) = \sum^{k}_{i=1} w_h(v_{i-1}, v_i) = \sum^{k}_{i=1} \left [ w_h(v_{i-1}, v_i) + h(v_{i-1}) – h(v_i) \right ] = \sum^{k}_{i=1} w_h(v_{i-1}, v_i) + h(v_0) - h(v_k) = \delta(p) + h(v_0) - h(v_k)\)
Hence, any path \(u \rightarrow v\) change the weight by the same offset \(h(u) – h(v)\) witch implies that the shortest path is preserved (but offseted).

Claim 2: If \(G\) has negative cycles, then there is no solution to the system \(w_h(u,v) =w(u,v) + h(u) – h(v) \geq 0\).

Let \(p: v_0 \rightarrow v_1 \rightarrow v_2 \rightarrow ... \rightarrow v_k \rightarrow v_0\) is a negative cycle and let’s assume that the system has a solution, then:
\(h(v_1) - h (v_0) \leq w(v_0,v_1)\)
\(h(v_2) - h (v_1) \leq w(v_1,v_2)\)
…
\(h(v_k) - h (v_{k-1}) \leq w(v_{k-1},v_{k})\)
\(h(v_0) - h (v_k) \leq w(v_k,v_0)\)
Adding these inequalities, we get: \(0 \leq w(v_0,v_1) + w(v_1,v_2) + . . . + w(v_{k-1},v_{k}) + w(v_k,v_0) \Rightarrow 0 \leq w(p)\) - is contradiction, hence the solution exists iff there is no negative cycle.

Claim 3: If we add a new node (let’s denoted it \(s\)) to \(G\) and a directed edge of weight 0 to eery node, then we claim that if \(h(v) = \delta(s, v)\) then \(w_h(u,v)=w(u,v) + h(u) - h(v) \geq 0\) for all \(u,v \in V\).

\(w(u,v) + h(u) - h(v) \geq 0\)
\(h(v) - h(u) \leq w(u,v) \Rightarrow \delta(s,v) - \delta(s,u) \leq w(u,v)\)
\(\delta(s,u) + w(u,v) \geq \delta(s,u)\)
\(\delta(s,v) - \delta(s,u) \leq w(u,v) \Leftrightarrow h(v) – h(u) \leq w(u,v)\)

The Johnson’s algorithm:

1. Add new node \(s\) to \(G\) and add an edge of weight \(0\) to every node and compute \(h(v) = \delta(s,v)\) for every node \(u \in V\) using Bellman-Ford. If there is a negative cycle, then Bellman-Ford will detect it.
2. Re-weight each edge with \(w_h(u,v)=w(u,v) + h(u) - h(v) \geq 0\).
3. Run Dijkstra from every node \(u \in V\) and compute all shortest paths.
4. Re-weight each edge with \(\delta(u,v) = \delta_h(u,v) - h(u) + h(v) \geq 0\).
   Done.

Implementation

tuple<bool, vector<vector<int>>>
	johnson(int n, vector<vector<pair<int, int>>>& adjL) {

	vector<vector<int>> d(n, vector<int>(n));
	bool cycle = false;

	// add new vertex (n) and edges with weight 0 to every other vertex
	vector<pair<int, int>> edges(n);
	for (int u = 0; u < n; u++) edges[u] = make_pair(u, 0);
	adjL.push_back(edges);	
	
	// Bellman-Ford and return function h
	vector<int> h;
	tie (cycle, h) = bellmanFord(n, n + 1, adjL);
	if (cycle) return make_pair(cycle, d);

	// remove vertex (n)
	h.pop_back(); adjL.pop_back();

	// Dijkstra on modified edges
	for (int u = 0; u < n; u++) {
		d[u] = dijkstra(u, n, adjL, h);
		
		// compute real distance
		for (int v = 0; v < n; v++)
			if (d[u][v] != INF) // is there a path
				d[u][v] = d[u][v] + (h[v] - h[u]);
	}

	return make_pair(cycle, d);
}

tuple<bool, vector<int>>
	bellmanFord(int start, int n, vector<vector<pair<int, int>>>& adjL) {

	bool cycle = false;
	vector<int> d(n, INF);
	d[start] = 0;

	for (int k = 1; k <= n - 1; k++) {
		for (int u = 0; u < n; u++) {
			if (d[u] == INF) continue;

			for (pair<int, int> p : adjL[u]) {
				int v = p.first;
				int w = p.second;

				d[v] = min(d[v], d[u] + w); // relaxation
			}
		}
	}

	// check for cycles
	for (int u = 0; u < n; u++) {
		if (d[u] == INF) continue;

		for (pair<int, int> p : adjL[u]) {
			int v = p.first;
			int w = p.second;
			if (d[v] > d[u] + w) {
				cycle = true; break;
			}
		}

		if (cycle) break;
	}

	return make_pair(cycle, d);
}

vector<int>
	dijkstra(int start, int n, vector<vector<pair<int, int>>>& adjL, vector<int>& h) {

	vector<bool> s(n, false);
	vector<int> d(n, INF);
	d[start] = 0;

	apqmin<int> q; // min priority queue
	for (int u = 0; u < n; u++) q.push(u, d[u]);

	while (!q.empty()) {
		int u = q.front(); q.pop();
		s[u] = true;
		if (d[u] == INF) continue;

		for (pair<int, int> p : adjL[u]) {
			int v = p.first;
			int w = p.second + (h[u] - h[v]);

			if (s[v] == true) continue;

			if (d[v] > d[u] + w) { // relaxation
				d[v] = d[u] + w;

				q.update(v, d[v]); // decrease priority
			}
		}
	}

	return d;
}

Complexity

\(T(V,E) = T_{Bellman-Ford} + V \cdot T_{Dijkstra} = O(VE + V^2log(V)) = O(V^2log(v))\) - for sparse graphs
\(T(V,E) = O(V^3log(v))\) - for dense graphs