Algorithm

Floyd-Warshall uses dynamic programming method to find all pairs shortest paths, but in a better way compare to Bellman-Ford in the sense that the sub-problems are built based on sub-sets of nodes rather than number of edges.
The general idea:

  • Initialize the estimated shortest distance between all pair of nodes without any intermediary node as \(d(u,v) = w(u,v)\);
  • Add nodes one by one to the set of internal nodes used within the shortest path and update the estimated shortest path between all pair of nodes considering the new path formed through the new added node;
  • The estimated shortest path for all pair of nodes is the shortest path when all the nodes are considered as internal nodes within the path.


The dynamic programming properties that Floyd-Warshall exhibits:

  • optimal substructure : for all pair of nodes \((u,v)\) find the shortest path from \(u\) to \(v\), so that all internal nodes within this path are from the set \({0, ...,k}\). Let’s denote the value of this path as \(d^{k}(u,v)\). We can calculate this path based only on \(d^{k-1}(u,k)\) and \(d^{k-1}(k,v)\).

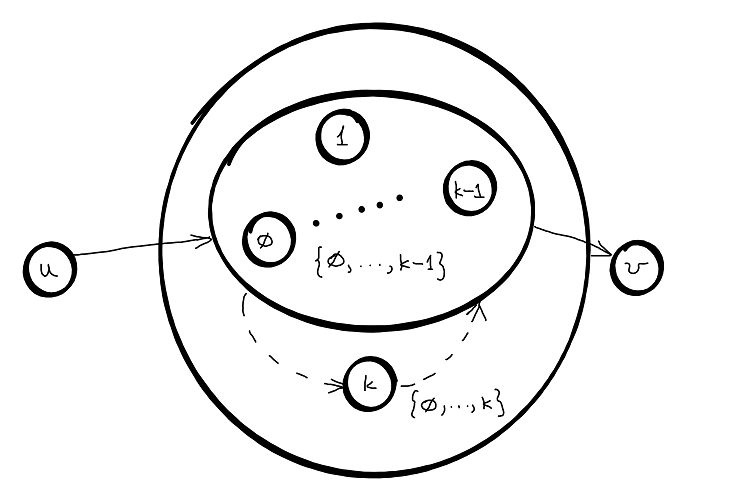
pic_01


  • case 1: we do not need node k
  • case 2: we need node k
    Choose the shortest between the two paths:
    \(d^{k}(u,v) = min \left \{ d^{k-1}(u,v), d^{k-1}(u,k) + d^{k-1}(k,v) \right \}\), for \(k = 0\) to \(V\)
    \(d^{\phi}(u,v) = w(u,v)\)
  • overlapping subproblems : \(d^{k-1}(u,k)\) is used to solve the problems for multiple \(v_j\) and \(d^{k-1}(k,v)\) is used to solve the problems for multiple \(u_j\).

Implementation

vector<vector<int>>
	floydWarshall(int n, vector<vector<int>>& adjM) {

	vector<vector<int>> d(adjM);

	for (int k = 0; k < n; k++) { // k = mid

		for (int u = 0; u < n; u++) {
			for (int v = 0; v < n; v++) {
				if (d[u][k] == INF || d[k][v] == INF) continue; // no path

				d[u][v] = min(d[u][v], d[u][k] + d[k][v]);
			}
		}

	}

	return d;
}

Note: As you can see, we do not need the third dimension when we build the shortest distances table because it is redundant. See the proof in the section below.

Example

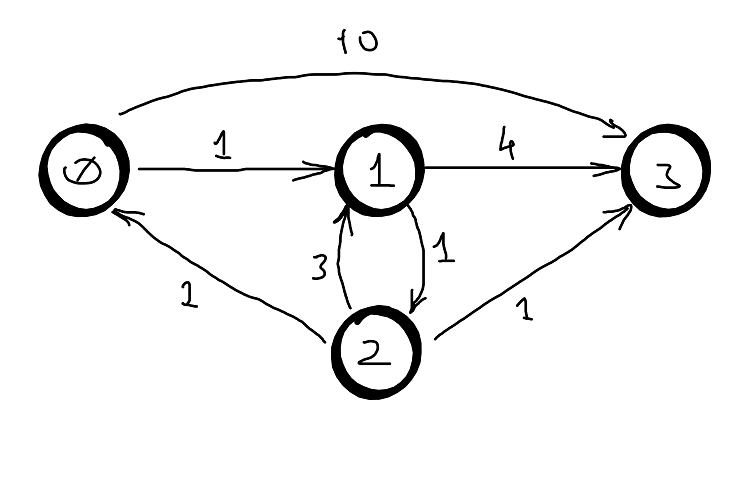
pic_02

— 0 1 2 3
0 0 1 inf 10
1 inf 0 1 4
2 1 3 0 1
3 inf inf inf 0
k=0 0 1 2 3
0 0 1 inf 10
1 inf 0 1 4
2 1 2 0 1
3 inf inf inf 0
k=1 0 1 2 3
0 0 1 2 5
1 inf 0 1 4
2 1 2 0 1
3 inf inf inf 0
k=2 0 1 2 3
0 0 1 2 3
1 2 0 1 2
2 1 2 0 1
3 inf inf inf 0
k=3 0 1 2 3
0 0 1 2 3
1 2 0 1 2
2 1 2 0 1
3 inf inf inf 0


Space optimization

We can drop the 3rd dimension of the distance table, because the \(k\) column and row does not change between iteration \(k – 1\) and \(k\).
\(d^{k}_{i,k} = min \left \{ d^{k-1}_{i,k}, d^{k-1}_{i,k} + d^{k-1}_{k,k} \right \} = min \left \{ d^{k-1}_{i,k}, d^{k-1}_{i,k} \right \} = d^{k-1}_{i,k}\)
\(d^{k}_{k,j} = min \left \{ d^{k-1}_{k,j}, d^{k-1}_{k,j} + d^{k-1}_{k,k} \right \} = min \left \{ d^{k-1}_{k,j}, d^{k-1}_{k,j} \right \} = d^{k-1}_{k,j}\)
This prove that the column and row \(k\) remains unchanged between consecutive iterations, hence we can drop the 3rd dimension.

Path Reconstruction

Exactly the same as for Generalization of Bellman-Ford :

  • \(pred[u][v] = pred[k][v]\);
  • \(next[u][v] = next[u][k]\);

Correctness (sketch)

Assume the graph does not contain negative cycles.
Inductive hypothesis: Suppose that we know all shortest paths for all pairs \(d^{k-1}(u,v)=\delta^{k-1}(u,v)\) that only uses nodes from the set \({0, ..., k-1}\).
Base case: \(d^{\phi}(u,v)=w(u,v)\) - direct edge (no node in between), the hypothesis holds.
Inductive step:: based on inductive hypothesis we will prove that \(d^{k}(u,v)=\delta^{k}(u,v)\).

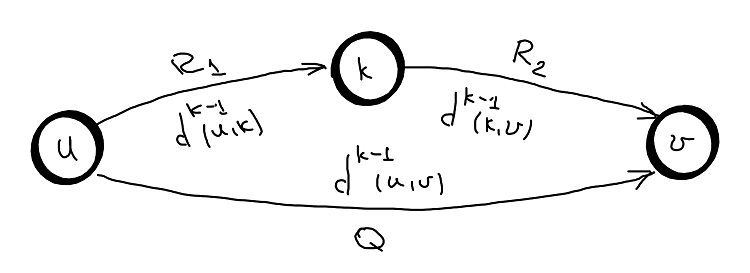
pic_03

The path from \(u \rightarrow k\) only uses nodes from the set \({0, ..., k-1}\).
The path from \(k \rightarrow v\) only uses nodes from the set \({0, ..., k-1}\).
Same from \(d^{k-1}(u,v)\).
The path \(P=R_1 + R_2\) containing node \(k\) is compared with the path \(Q\) which does not contain node \(k\) and the shortest is the \(\delta^{k}(u,v)\). So:
a. the path from \(u \rightarrow v\) without node \(k\) was found in previous iteration (\(k – 1\)).
b. the paths from \(u \rightarrow k\) and \(k \rightarrow v\) were also found in previous iteration (\(k – 1\)).
Hence, from a and b the update ensure that the induction hypothesis holds after iteration \(k\).

Complexity

Time and space complexity are trivial: \(T(V,E) = O(V^3)\) and \(S(V,E) = O(V^2)\).

Negative Cycle Detection

Just as Generalization of Bellman-Ford , Floyd-Warshall also detects negative cycles. If a shorter path exists after \(V-1\) iterations, then the graph must contain a negative cycle, which basically means that there is a loop from \(v\) to \(v\) that is less than \(0\), so the distance matrix must contain some value less than \(0\) on its diagonal.

Miscellaneous (the memoization version)

When the tabulation method is used, the distances are constructed from bottom-up on the set of internal nodes, but the when the memoization method is used the distances are arbitrary. So, for memoization we need the third dimension for the table.

vector<vector<int>>
	FloydWarshallMemo(int n, vector<vector<int>>& adjM) {

	vector<vector<vector<int>>> memo(n + 1, vector<vector<int>>(n, vector<int>(n, INF)));
	for (int u = 0; u < n; u++)
		for (int v = 0; v < n; v++)
			FloydWarshallMemo(n, u, v, n, adjM, memo);

	return memo[n];
}

int FloydWarshallMemo(int k, int u, int v, int n, vector<vector<int>>& adjM, vector<vector<vector<int>>>& memo) {
	if (memo[k][u][v] != INF) return memo[k][u][v];

	if (u == v) memo[k][u][v] = 0;
	else if (k == 0) memo[k][u][v] = adjM[u][v];
	else {
		int uv = FloydWarshallMemo(k - 1, u    , v    , n, adjM, memo);
		int uk = FloydWarshallMemo(k - 1, u    , k - 1, n, adjM, memo);
		int kv = FloydWarshallMemo(k - 1, k - 1, v    , n, adjM, memo);
	
		if (uk == INF || kv == INF) memo[k][u][v] = uv;
		else memo[k][u][v] = min(uv, uk + kv);
	}

	return memo[k][u][v];
}

Note: For reference, see Bellman-Ford memoization version .